The VBA development environment - called Visual Basic Editor (VBE) - is where you will write and verify the code to perform Excel actions. There are a few ways to open the VBE:
+
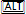You can also open VBE from the View tab $\rightarrow$ Macros, creating a new macro.
The VBE framework has several internal windows, the main ones being:
Advanced topics are recommended only after acquiring some experience in the subject. They are made available due to their proximity to the theme.
If any window does not appear, just enable it in the tab View $\rightarrow$ 'Desired Window'.
Initially we will use (1.) Project Explorer, (2.) Code Window, (3.) Toolbar and (4.) Menu bar windows.
We will gradually understand the function of each of these windows.
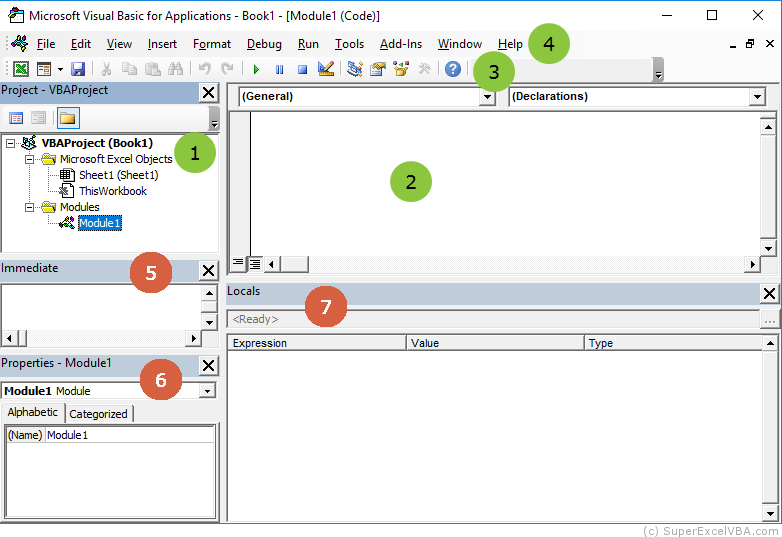
The Project Explorer or Project - VBAProject is the VBE window that lists hierarchically the loaded projects.
The VBAProject is created along with the Excel document (file) and every document has only one project.
In the example above, we have two projects, so we can immediately conclude that there are two open files in Excel (
Products.xlsm and Sales.xlsm). Note that VBE separates content into folders for organizing purposes.
Every VBA code resides inside an item in the VBE Project Explorer. The Code Window will show the VBA code that is within the selected item in the Project Explorer.
The Code Window is where all VBA code will be displayed and developed.
Every Macro will always be written in this window and will reside inside an item in the Project Explorer.
To open a Code Window double click on the desired item in the Project Explorer window.
The Toolbar provides some essential options for the project (buttons such as 
Undo and 
Save). There are also on this bar buttons to execute the code (such as Run Macro and Reset) and help for creating codes (such as 
Find and 
Paste).
It is possible to edit the Toolbar. You may add for example the edit buttons tab, which allow commenting on a block of text (View $\rightarrow$ Toolbars $\rightarrow$ Edit).
The Menu bar lists the features of the VBE.
When you are having trouble finding some functionality in the Toolbar, you may choose to browse the menus in the Menu bar.
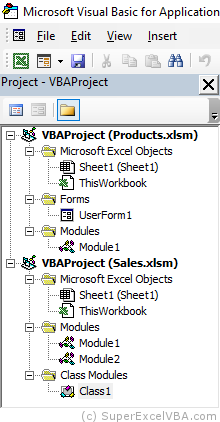
A Module is a place for you to store codes.
In general, macros are written in modules.
Further ahead we will see cases where the code is inserted into other Project Explorer items.
To create a Module (with VBE open):
Try to use the modules when writing your macros.
SuperExcelVBA.com is learning website. Examples might be simplified to improve reading and basic understanding. Tutorials, references, and examples are constantly reviewed to avoid errors, but we cannot warrant full correctness of all content. All Rights Reserved.
Excel ® is a registered trademark of the Microsoft Corporation.
© 2024 SuperExcelVBA | ABOUT
